Fourier optics, as introduced in the text book Fourier Optics by John Goodman, provides a framework for analyzing optical systems. Optical sources generate aperture fields, which then propagate freely until some configuration of optical elements generates a new aperture field. The essential feature is a separation of the field-propagation and the field-interaction operations. The split-step method of integrating the FPE uses the same separation. The scheme is mathematically tractable because the field propagation and interaction operations can be implemented with extremely sparse wavelength sampling. However, there are limitations as demonstrated in the paper Spherical Wave and Plane Wave Propagation.
Ray theory takes the very different approach of identifying ray paths normal to wave fronts. Ray paths connect source and destination points within the medium. The development of ray occupies the the first half of the seminal textbook The Principles of Optics by Born and Wolf. Equation (3.2.2) captures the essential elements of ray optics for scalar waves. Although any propagation medium is populated by an infinity of ray paths, if an excitation field concentrates the field into a directed narrow beam, a single or small number of ray paths will trace the propagation of the beam.
Seminal treatments of propagation in the earth’s ionosphere include The Propagation of Radio Waves…, by K. G. Budden, Theory of Ionospheric Waves, by K. C. Yeh and C. H. Liu, and Ionospheric Radio Propagation, by Kenneth Davies. Each of these texts summarizes the propagation of pane waves in in-homogeneous an-isotropic media The theory is in two parts. The physics of magnetically biased plasma is applied to determine the susceptibility tensor. The Appleton-Hartree equations, which are summarized in the appendix to Rino and Carrano, characterize the propagation of plane electromagnetic waves in a homogeneous an-isotropic media. The first 11 chapters of Budden and the first 4 chapters of Yeh and Liu are devoted to propagation in uniform or stratified media. Ray optics treatments start with a derivation of the eikonal equation, but it is used mainly to develop the properties of rays and ray bundles, rather than the computation rays in in homogeneous media. Once the properties of Rays are established, approximations as summarized in the applications-oriented treatment by Davies suffice.
Ray computation is not introduced until Budden’s Chapter 14. It is not until Budden’s Chapter 14.5 that the Haselgrove form of the equations are summarized. In homogeneous media a vanishing 3 dimensional determinant has only two solutions, which identify the characteristic modes. In an in-homogeneous medium the eikonal itself appears in a vanishing determinant, which leads to two partial differential equations, which must be solved to determine the ray paths followed by characteristic modes. This can be seen most directly in the review paper by Christopher Coleman following Equation (11). The challenge is the solution of such partial differential equations, which is treated in Volume II of the graduate-level text books by Curant and Hilbert. However, if the magnetic field is turned off, the susceptibility matrix becomes diagonal and the ray trace solution defaults to the scalar form (Born and Wolf. Equation (3.2.2)), which is amenable to much simpler treatment.
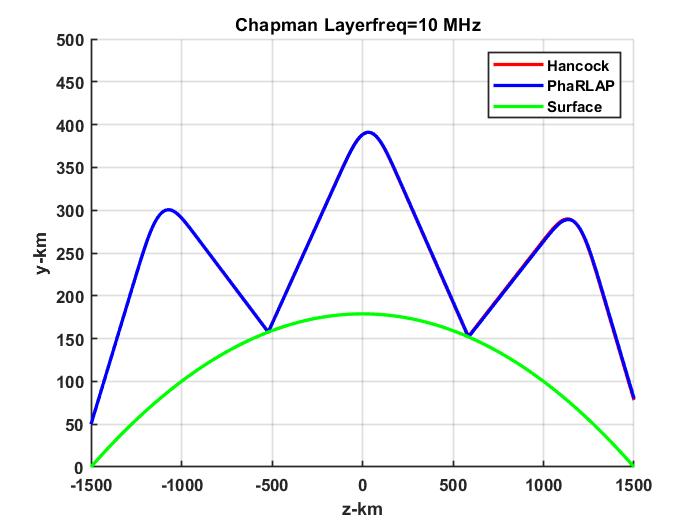
There is a further complication with near-earth radio wave propagation, namely reflection of downward propagation waves that intercept the earth’s surface. To the extend that the earth is a smoothly varying conducting surface, a ray intercepting the earth is simply redirected upward about the surface normal. Treating the earth surface as spherical allows for straightforward analytic treatment of both surface reflections an radially varying ionospheric density profiles. PHaRLAP is a 3-D magnetoionic Hamiltonian ray tracing engine developed by the Australian Defence Science and Technology Organisation (DSTO). A scalar version of the code has been adapted from a scalar ray trace code developed by Dennis Hancock. The figure below shows a ray comparison of PHaRLAP with B=0 and Hancock scalar ray trace results, which are indistinguishable.
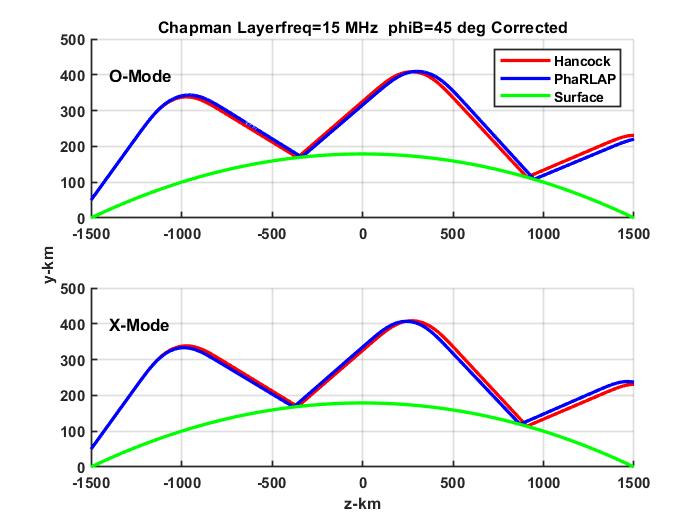
The scalar ray trace has been used with the O and X mode refractive indices from the Appleton-Hartree equations. (See Tsai, et al.) Two examples are shown below: