This website has been dormant since 2015. The website was started as a platform for discussion related to my book published in 2011. I have removed some of the blogs, which are out of date. Blogs that clarified topics in the book, identified errors, and introduced related topics have been retained.
To put this in perspective, the first two book chapters laid the foundation for a complete theory of scintillation, which follows from the forward propagation equation (FPE). Briefly, for propagation studies Maxwell’s equations are used to derive second-order differential equations that characterize electromagnetic (EM) wave propagation, which are known to engineers as the Helmholtz equation. However, the Helmholtz equation characterizes EM fields emanating from a collection of interacting point sources. The problem of interest involves calculating the propagation of an EM field from the phase center of a transmitting antenna to the phase center of a receiving antenna.
To put the Helmholtz equation in a more directly applicable form, it is rewritten as a pair of coupled first-order differential equations that individually characterize EM waves propagating in opposite directions along the reference direction defined by the ray connecting antenna phase centers. A well-designed radio transmission and reception system will maximize the energy collected at the receiver. The FPE characterizes the field launched at the transmitter the intercepts the phase center of the receiving antenna. A further simplification calculates time-harmonic fields, which generally capture all that is needed to calculate signal amplitude, phase, and delay perturbations. The FPE is exceptionally well suited for calculating propagation effects induces by ionospheric structure intercepted along the propagation path.
As a first-order differential equation, the FPE can be integrated to generate a realization of the propagating EM field. However, his requires a model of the ionospheric structure. This information comes from three sources:
- Purely statistical models that impose an amplitude weighting on independent Fourier modes.
- Physics-based simulations of ionospheric structure.
- Configuration space models
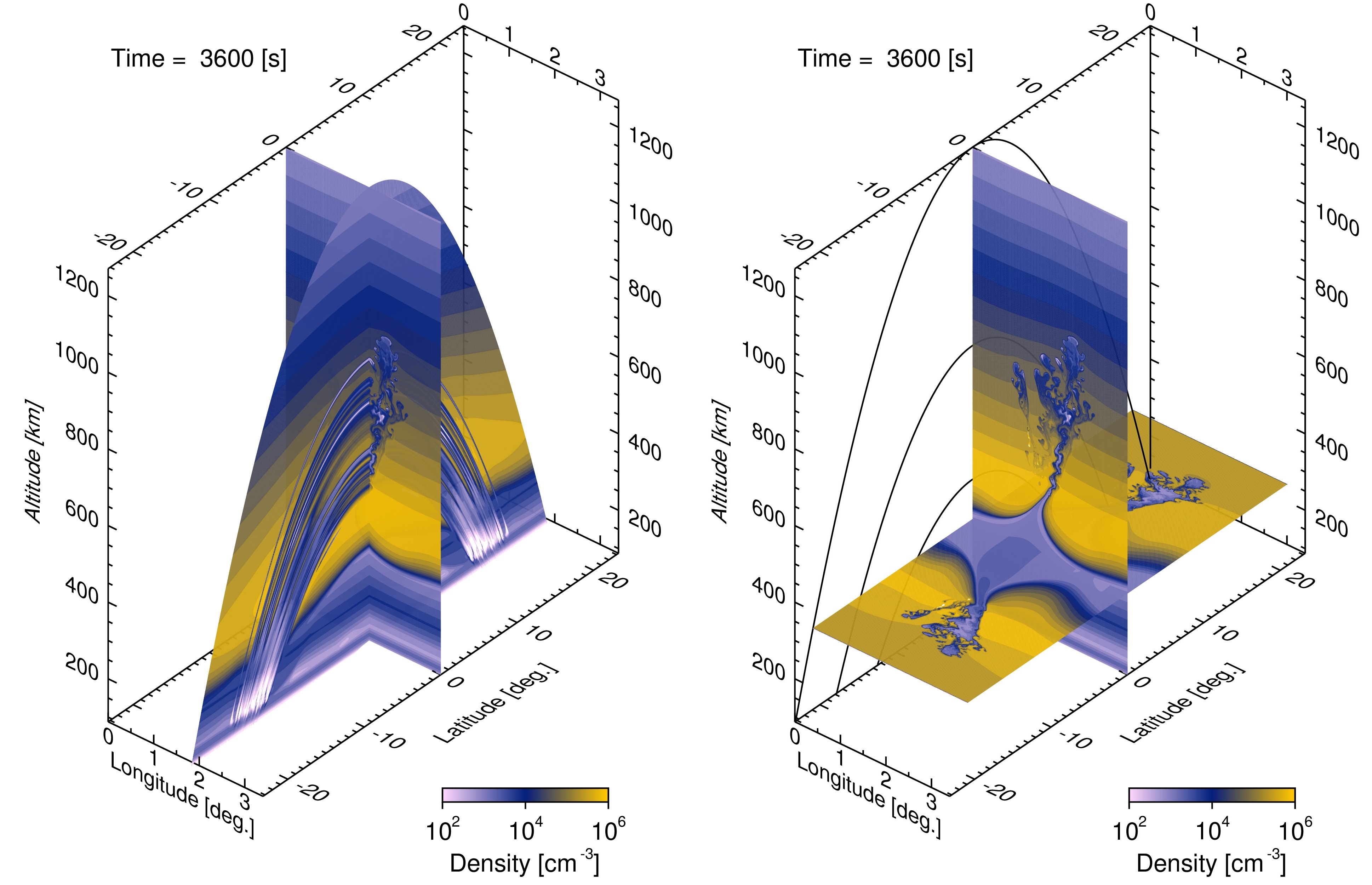
Only purely statistical models were introduced in the book. To accommodate field-aligned anisotropy, the spherical isotropic surfaces of constant spatial coherence are transformed into elongated surfaces, generally ellipsoids. Additionally, because the transmission paths of primary interest were from earth-orbiting satellites to near-earth receivers, an ionospheric topocentric coordinate system with downward, northward, and eastward reference axes was introduced. In a downward oriented coordinate system satellite to earth propagation paths intercept the earth’s surface a very large distances from the nadir point. For efficient computation the integration is performed in a continuously displace coordinate (CDP) system that follows the reference ray. Chapter 4 in the book developed all the necessary geometric manipulations. The oblique propagation blog introduces supplemental material to clarifying how CDP coordinates are introduced into moment equations.
While scintillation theory follows from solutions to the FPE, characterizing stochastic structure requires statistical measures. Statistically homogeneous processes are characterized by spectral density functions (SDFs), which is formally ensemble averages of the intensity of spatial Fourier transformations of the structure realizations. Chapter 3 reviews the most widely used statistical theory, which introduces a hierarchy of differential equations that statistical observables to functions of the structure SDF. While much has been learned from solutions to the fourth-order moment equation that characterizes intensity scintillation, the computation involved is too demanding for interpreting diagnostic measurements.
A time-honored simplification is the equivalent phase screen, which concentrates the structure into an equivalent path-integrated phase screen. Under the narrow-angle scatter or parabolic approximation forward propagation is completely specified by the Fresnel scale. The scintillation at a fixed distance from the phase screen is reproduced at a different frequency and propagation distance that keeps the Fresnel scale constant. The FPE becomes the more familiar parabolic wave equation (PWE). Moreover, the scintillation intensity SDF (and scintillation index S4) can be computed a function derived from the structure SDF. The Phase Screen Models for Numerical Computation blog includes a compact summary of the material.
The material in Chapter 4 influenced the development of a simulation model called SIGMA Dispande. The phase-screen model was used to simulate the GPS effects of scintillation on GPS signals Ghafoori
Chapter 5 addresses system applications, which include signal processing for scintillation diagnostics. Beacon satellite diagnostic receivers transmit VHF, UHF, and L-band signals. Digital receives generate frequency-dependent amplitude and phase histories. The phase data are dominated by changing range, which can introduce Doppler shifts exceeding 12 kHz. To measure the scintillation component, it is necessary to isolate the Doppler component. One method is to implement a digital phase locked loop (PLL). However, the order of the PLL determines the number of samples used to estimate the frequency or phase. A more robust procedure that allows an arbitrary number of samples is described in the Digital Signal Processing and A Comparison of Phase Locked Loops and Frequency Hypothesis Testing blogs. The blog AGU 2013 Poster and Supplemental Material describes a true tomographic reconstruction, which is mainly of academic interest because of the sampling requirements.
Chapter 5 also introduced some diagnostic signal processing procedures and a supplemental MatLab library. Simulated complex scintillation requires no detrending. For plane-wave excitation the average signal intensity is constant, which is most conveniently set to unity. Real intensity scintillation measurements vary because of path-loss associated with changing range and antenna pattern variations. A Butterworth filter is typically used to make a rigid frequency separation between the signal mean and the structure component. One problem with this approach is that the detrend interval should be data driven and an large as possible. While it is true that Fresnel filtering suppresses large scale variation, the cutoff is not rigid and level dependent. We find that wavelet-based filters are easier to implement and more flexible. Simulated phase scintillation requires no detrending. Real phase scintillation data is dominated by the geometric path variation. The problem there is you cannot separate the geometric contribution from total electron content variation, which is the reason navigation satellites use multi-frequency transmissions. These issues will be discussed in separate blog entries.
What amounts to a GPS Toolbox, which is an upgrade of resources originally developed for low-earth-orbit (LEO) beacon data, contains orbit prediction from ephemeris elements, magnetic field computation, and GPS coordinate manipulation. Scintillation utilities provide all the geometric transformations needed to accommodate field-aligned geometry dependencies. A wavelet library provides all the MatLab utilities needed for wavelet based detrending and segmentation applications.