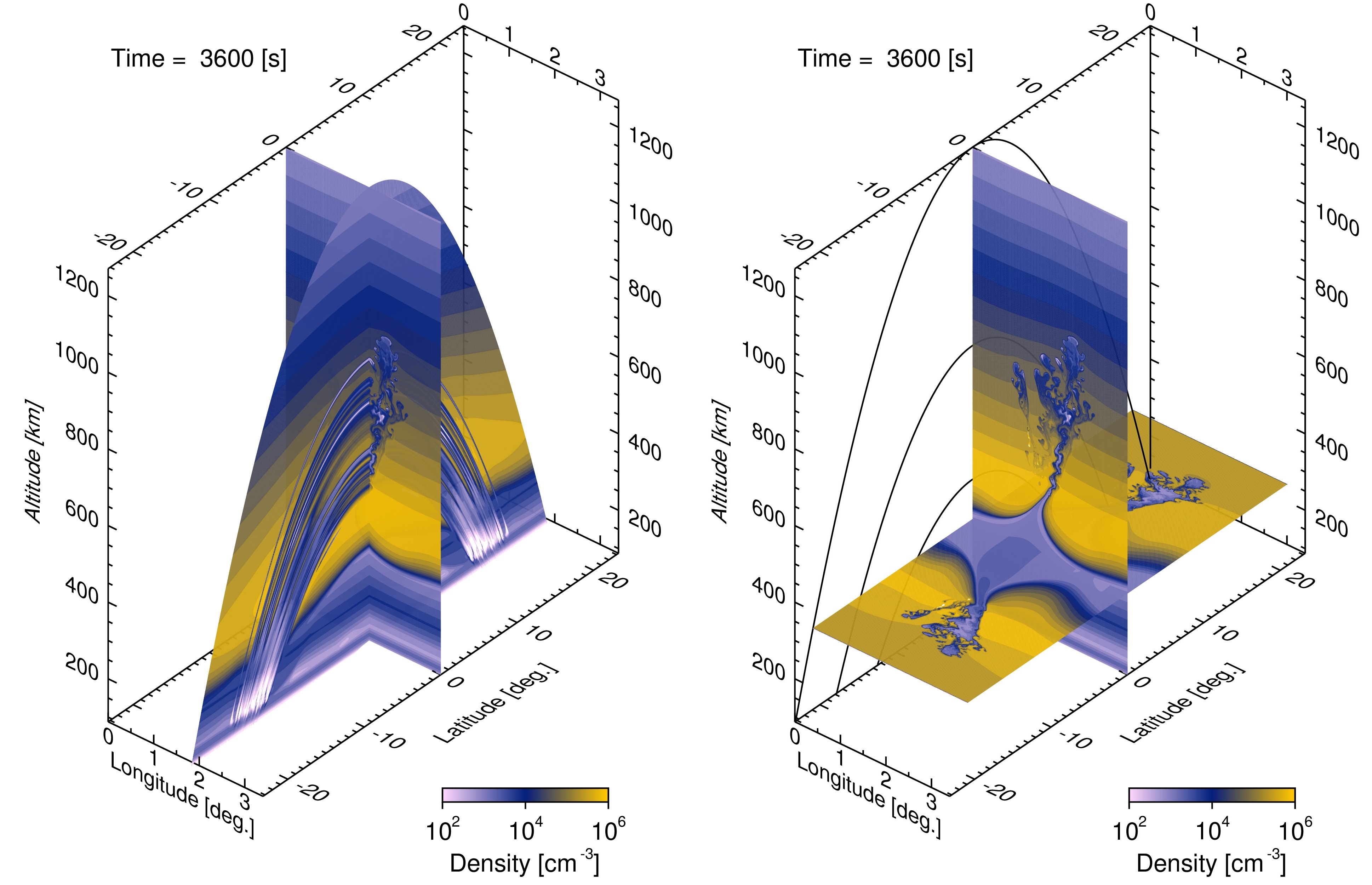
Following the post Limitations of the Forward Approximation, which dealt with the pitfalls of extending the forward approximation to HF, the applications of the statistical theory dealing with near line-of-sight propagation at frequencies from VHF to S-Band. The upper limit is imposed because neutral atmospheric effects, particularly precipitation, dominate propagation disturbances. Morphological studies of scintillation have been pursued since the 1950s using extraterrestrial radio stars. Prior to satellite observations following Sputnik in 1957, signal intensity fluctuations were the only diagnostic. Diagnostic measures included intensity moments, probability density functions (PDF), and spectral density functions (SDFs), which is the power spectrum of intensity about the estimated mean. The moments of a random variable formally define the PDF. Any integrable non-negative function defines a PDF. A small number of PDFs are defined by low order moments.
Whereas gaussian processes have a prominent role in communication theory, scintillation statistics are non-gaussian and require at least three moments. However, aside from the fade distribution, the statistical theory of scintillation does provide at parameterized theoretical model of the SDF in terms of a parameterized path-integrated electron density SDF. Because of the analytic complexity only the weak scintillation form is typically used. It is generally accepted that electron density structure has a turbulence-like inverse power law form, but few attempts have been made to generate structure diagnostics that connect directly to the physical observables that characterize the structure.
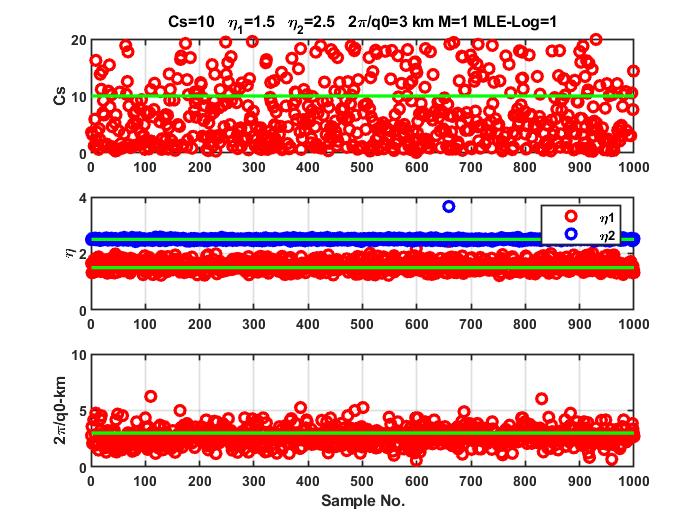
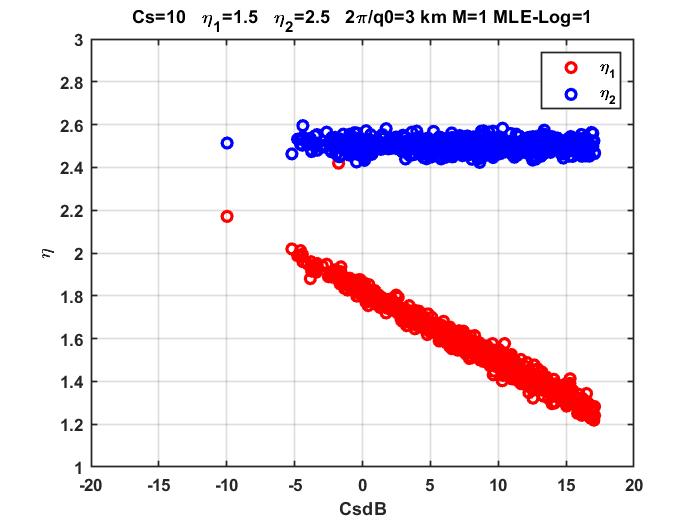
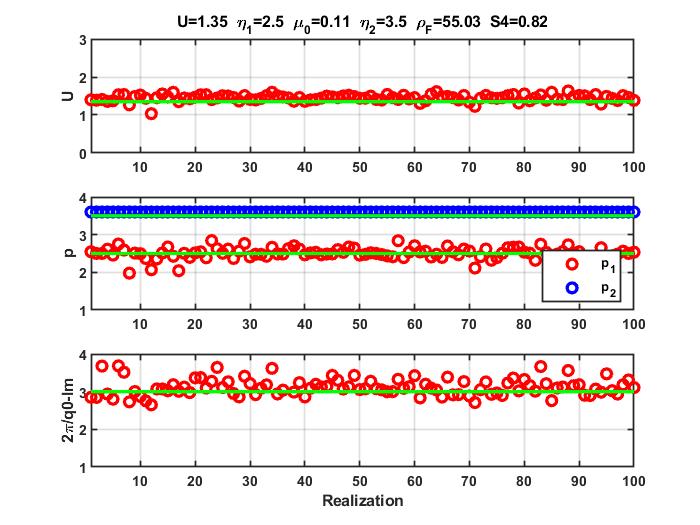
Our paper On Phase Screen Models for Scintillation Diagnostics, which has been accepted for publication pending minor changes, is an attempt to provide a unified parameterized theory that predicts the intensity SDF (Equation (32)) and per force the intensity scintillation index (Equation (35)). The theory also predicts the mutual coherence function (MCF) of the complex signal, which is functionally related to the phase structure function (Equation (30)). The mutual coherence function is defined by the power spectral density (PSD) of the complex signal. The ROTI diagnostic for a specified phase separation is a single value of the phase structure function. Consequently, the same theory that predicts the intensity SDF and S4 also predicts ROTI.
Regarding phase, there are some caveats. There is not theory beyond the weak-scintillation limit that predicts scintillation phase. All studies of phase structure are based on multiple phase screen (MPS) or equivalent phase screen simulations. Moreover, to the extent that phase scintillation admits an analytic characterization the inverse power-law form implies that phase variance is dominated by the large-scale structure and thereby acutely sensitive to the large-scale power-law index and the interval over which it is measured.
Our paper demonstrates the interrelations, and the effects of additive noise can be assessed quantitatively in terms of an estimate of an effective signal-to-noise ratio (SNR) derived from the detrended intensity. Work in progress is exploring refined structure diagnostics derived from back propagation.