Scintillation history published in “100 Years of the International Union of Radio Science https://chuckrino.com/wp-content/uploads/2022/07/ScintillationHistory.pdf
Keynote talk: https://chuckrino.com/wp-content/uploads/2022/07/KeynoteTalkBSS2022S.pptx
In HF Propagation we described the extension of the scalar forward propagation equations (FPE) to accommodate HF propagation in the ionosphere where polarization effects important. Looking ahead to comparing full-field simulations to ray trace results we introduced ray tracing. In a delayed companion paper, Rino and Corrano currently in review, we introduced surface reflections to generate a complete vector forward propagation equation (VFPE). Accommodating surface reflections used an application of the forward approximation to surface scatter, Rino et al.
The following figure (Figure 4 in the paper) summarizes a VFPE realization. The upper frame is a static display of the field intensity evolving from and narrow upward point beam at z=-1500 km. The lower frame shows the spectral density of the field plotted against normalized spatial wave number, which is a measure of propagation direction. The upward trajectory is refracted by the ionosphere, redirecting the beam toward the earth’s surface where it is reflected. The details of the reflection are shown in the movie display.
The figure below (Figure 8 in the paper) shows a comparison of trace of orthogonal polarized signal peaks with an overlay of the trace obtained from the PHaRLAP ray trace program as described in the paper. However, to get the agreement a correction to the VFPE was necessary. As described in the paper the was guess based sole on the behavior or the displacement as described in the paper. An argument was made as to why there should be a difference between a ray trace and realizations derived from the VFPE. The key element is the separate application of the propagation and refraction operations in each computation cycle. We expect further discussion and development of this new finding.
Fourier optics, as introduced in the text book Fourier Optics by John Goodman, provides a framework for analyzing optical systems. Optical sources generate aperture fields, which then propagate freely until some configuration of optical elements generates a new aperture field. The essential feature is a separation of the field-propagation and the field-interaction operations. The split-step method of integrating the FPE uses the same separation. The scheme is mathematically tractable because the field propagation and interaction operations can be implemented with extremely sparse wavelength sampling. However, there are limitations as demonstrated in the paper Spherical Wave and Plane Wave Propagation.
Ray theory takes the very different approach of identifying ray paths normal to wave fronts. Ray paths connect source and destination points within the medium. The development of ray occupies the the first half of the seminal textbook The Principles of Optics by Born and Wolf. Equation (3.2.2) captures the essential elements of ray optics for scalar waves. Although any propagation medium is populated by an infinity of ray paths, if an excitation field concentrates the field into a directed narrow beam, a single or small number of ray paths will trace the propagation of the beam.
Seminal treatments of propagation in the earth’s ionosphere include The Propagation of Radio Waves…, by K. G. Budden, Theory of Ionospheric Waves, by K. C. Yeh and C. H. Liu, and Ionospheric Radio Propagation, by Kenneth Davies. Each of these texts summarizes the propagation of pane waves in in-homogeneous an-isotropic media The theory is in two parts. The physics of magnetically biased plasma is applied to determine the susceptibility tensor. The Appleton-Hartree equations, which are summarized in the appendix to Rino and Carrano, characterize the propagation of plane electromagnetic waves in a homogeneous an-isotropic media. The first 11 chapters of Budden and the first 4 chapters of Yeh and Liu are devoted to propagation in uniform or stratified media. Ray optics treatments start with a derivation of the eikonal equation, but it is used mainly to develop the properties of rays and ray bundles, rather than the computation rays in in homogeneous media. Once the properties of Rays are established, approximations as summarized in the applications-oriented treatment by Davies suffice.
Ray computation is not introduced until Budden’s Chapter 14. It is not until Budden’s Chapter 14.5 that the Haselgrove form of the equations are summarized. In homogeneous media a vanishing 3 dimensional determinant has only two solutions, which identify the characteristic modes. In an in-homogeneous medium the eikonal itself appears in a vanishing determinant, which leads to two partial differential equations, which must be solved to determine the ray paths followed by characteristic modes. This can be seen most directly in the review paper by Christopher Coleman following Equation (11). The challenge is the solution of such partial differential equations, which is treated in Volume II of the graduate-level text books by Curant and Hilbert. However, if the magnetic field is turned off, the susceptibility matrix becomes diagonal and the ray trace solution defaults to the scalar form (Born and Wolf. Equation (3.2.2)), which is amenable to much simpler treatment.
There is a further complication with near-earth radio wave propagation, namely reflection of downward propagation waves that intercept the earth’s surface. To the extend that the earth is a smoothly varying conducting surface, a ray intercepting the earth is simply redirected upward about the surface normal. Treating the earth surface as spherical allows for straightforward analytic treatment of both surface reflections an radially varying ionospheric density profiles. PHaRLAP is a 3-D magnetoionic Hamiltonian ray tracing engine developed by the Australian Defence Science and Technology Organisation (DSTO). A scalar version of the code has been adapted from a scalar ray trace code developed by Dennis Hancock. The figure below shows a ray comparison of PHaRLAP with B=0 and Hancock scalar ray trace results, which are indistinguishable.
The scalar ray trace has been used with the O and X mode refractive indices from the Appleton-Hartree equations. (See Tsai, et al.) Two examples are shown below:
All of the analysis summarized on this website thus far has been based on the scalar wave equation, which ignores polarization. The constitutive relation is a temporally and spatially varying complex scalar function. The scalar function was introduced in The Theory of Scintillation as a refractive index. However, that identification is dependent upon the assumption that fields in transparent in-homogeneous media are locally plane-wave-like. The formal connection is via a separately computed phase function referred to as the eikonal. The constitutive relation in Maxwell’s equations is the dielectric susceptibility. More accurately stated, the scalar wave equation characterizes the interaction of an electric field with a medium defined by a spatially and temporally varying susceptibility. When the time variation is slow compared to the propagation time from a source to a point of reception, the time-harmonic form of of the wave equation, e. g. Equation (2.1) in The Theory of Scintillation, is the formal starting point for analysis. The frequency range is close to or exceeding 100 MHz.
The historically named High Frequency (HF) range from 3 to 30 MHz is a legacy of the discovery of the ionosphere from radio propagation observations. The HF band supports long-range communication via refractive redirection of signals that would otherwise propagate into space. At HF frequencies the scalar susceptibility must be replaced by a 3×3 tensor, which continually transforms the vector electric field, thereby introducing an evolving polarization of the propagating wave field.
The theory of HF propagation has been treated extensively. However, full-field simulations of realistic propagation environments have been computationally prohibitive except for highly idealized environments. The same would be true for the scalar theory were it not for the forward approximation, introduced in Chapter 2 of The Theory of Scintillation. The forward approximation reduces the solution of the second-order propagation differential equation to two coupled first-order differential equations, which individually characterize waves propagating in the forward and backward directions. In the spatial Fourier domain the respective plane-wave vectors have only positive or negative components along a reference axis connecting a plane containing the source with a parallel but displaced observation plane. The forward approximation neglects backward propagating waves, whereby propagation in an in-homogeneous medium is characterized by integrating a first-order differential equation. The split-step method starts with a local phase perturbation followed by a propagation operation. This is referred to as the multiple-phase-screen method.
The theory of scintillation is based on the forward approximation, which can be further simplified by assuming that the propagating waves are confined to a narrow cone of propagation angles. In that case the propagation operator admits a form that can be evaluated in the spatial domain. This simplification makes the statistical theory of scintillation, as summarized in Chapter 3 of The Theory of Scintillation, analytically tractable. However, with modern computational resources simulations without the narrow-angle-scatter constraint are feasible. At HF frequencies refraction can change the propagation direction significantly, whereby narrow-angle-scatter is violated.
It is desirable to exploit the FPE advantages at HF frequencies. To do so the scalar susceptibility must be replaces with its tensor form. Following the same steps used to derived the scalar FPE one obtains three coupled first-order differential equations. Upon computing the eigenvector decomposition of the susceptibility tensor and transforming the fields the coupling is removed whereby the transformed equations can be integrated. The original fields are then reconstructed by applying the inverse transformation. In a recently published paper, Rino and Carrano, we developed and demonstrated a vector forward propagation equation (VFPE), as defined by Equations (350 and (36) in the paper.
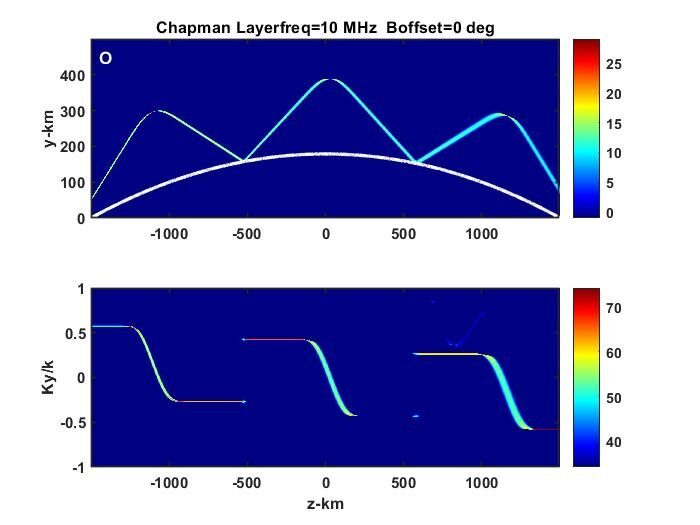
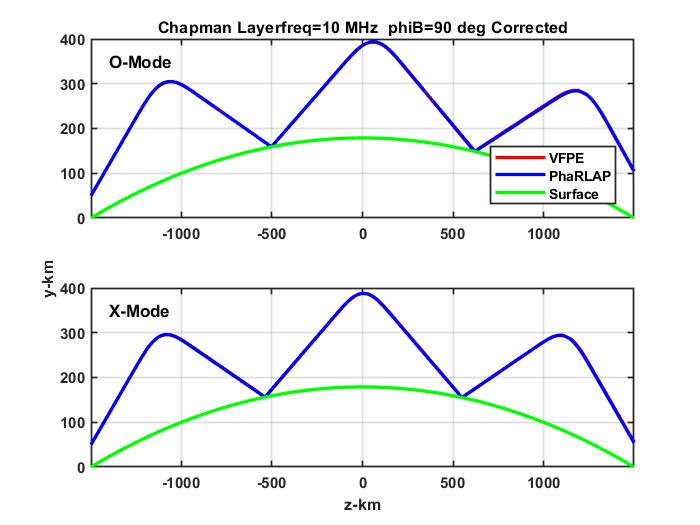
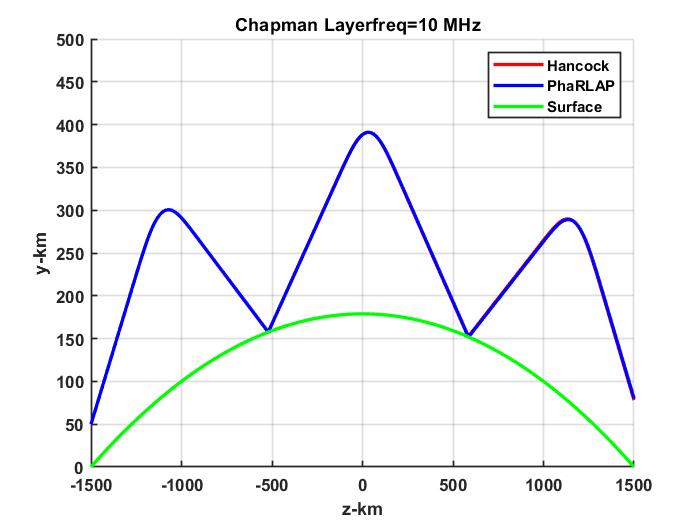
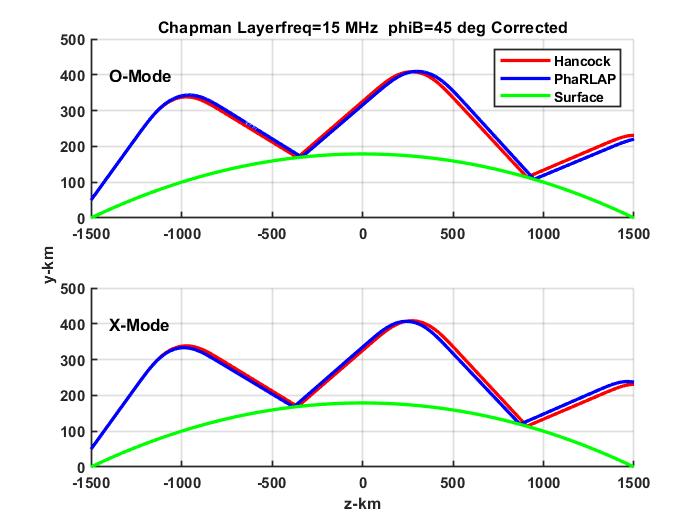
We showed that in a propagation environment with sufficient regularity, that is no structure variation transverse to the propagation direction, solutions to the FPE can be constructed as summations of X and O characteristic modes (Figures 2 and 5 in the paper). Launching a narrow beam upward into an ionospheric Chapman-layer distribution, we found that the beam refracted back toward the surface is comprised of two orthogonally polarized components (Figures 10 and 11 in the paper).
The intensity peak and propagation direction, which is defined by a complementary Fourier domain peak, effectively define ray paths, which can be compared to ray theory. A second paper currently under review carried out that extension. However, before describing the results it is helpful to review ray theory and its relation to VFPE realizations.
Previous blogs have outlined the development of irregularity parameter estimation (IPE) as applied to ionospheric scintillation data and to simulations as described in Rino and Carrano and Rino, Carrano, and Yokoyama, respectively. The applications of IPE assume diagnostic measurements are characterized by two-component power-law SDFs. The theory of stochastic processes provides a framework for generating abstract realizations of processes that have statistically similar coherence properties. However, the physical phenomenon of interest is the evolving three-dimensional ionospheric irregularity structure, particularly equatorial spread F which refers to diagnostic HF sounder back scatter from equatorial plasma bubbles (EPBs).
Whereas the structure that immediately identifies EPBs depends on configuration, SDFs ignore the phase of the Fourier components that define the structure. Furthermore, Fourier components that equate wavelength and structure scale are not physically realizable. Configuration-space models use random configurations of three-dimensional physically realizations of striations with definitive scales as described in Rino and Carrano. The fact that the configuration space-model provides both physical realizations and SDFs makes it ideally suited for validating propagation models, which start with three-dimensional structure models an predict diagnostic measurements. Of particular interest are two-dimensional propagation models and the equivalent phase-screen model. The interrelations are developed in Rino and Carrano.
Most recently we have begun to consider some broader issues regarding structure models. Ionospheric physics is concerned with all aspects of the earth’s ionosphere, which are generally manifest in changes of the electron density as a function of position and time. Ionospheric models capture the attributes that can be represented with parameterized mathematical expressions. These quasi-equilibrium models provide starting point for incorporating ionospheric disturbances, which may themselves admit analytic characterization. Internal waves provide an example. Stochastic structure does not admit direct mathematical realization except through physics-based simulations. Furthermore, there is no definitive scale at which structure transitions from quasi-deterministic to stochastic. In a diagnostic measurement segments that support stochastic characterization must be identified. More formally, the density structure must be broken down by scale. At some point in this process the sub structure is effectively stochastic and locally in-homogeneous.
An approach to ionospheric modeling and segmentation was introduced at a Living With a Star workshop presentation. A detailed discussion can be found in an unpublished note. With the global ionospheric coverage provided through the GNSS satellites, direct measurement of total electron content (TEC) is particularly appealing. In particular, the gigahertz frequencies used by the GNSS satellites is by design minimally affected by scintillation. By design GNSS satellites are minimally affected by propagation disturbances, whereby global TEC observations can be processed to extract stochastic structure, as described in Rino et al.
An enduring challenge in characterizing ionospheric intermediate-scale irregularity structure is generating a three-dimensional model. In-situ measurements provide one-dimensional scans, which must be reconciled with a higher dimensional model. Physics-based three-dimensional realizations of the development of equatorial plasma bubbles have been used for some time, but until recent work by Tatsuhiro Yokoyama . Tasuhiro has generously made his high-resolution simulations available for structure characterization. The results are presented in a published paper.
The image below shows a perspective view of the three-dimensional structure at a late phase in the development. The stochastic structure is confined to two-dimensional slice planes that intercept the field lines that terminate at low altitudes in opposite hemispheres.
Stochastic structure models typically assume an-isotropic structure in three dimensions. However, at some point, the quasi-deterministic field-aligned structure structure become important, which will be addressed in a later blog.
The classification in the paper is confined to time and height dependence as measured in slice planes. A graphic examples of the structure development is show in the movie.
Irregularity parameter Estimation (IPE) was developed for estimating the intensity SDF from detrended intensity scintillation measurements. As discussed in the blog, the original IPE procedure was replaced with an improved maximum likelihood estimator (MLE). The MLE scheme was also used in the analysis described in the previous blog. A common MatLab library of software was developed for both IPE applications. An unpublished report summarizes the results and describes the describes the library.
The first two figure frames below, which are taken from the paper show the four two-component power-law parameter estimates and a scatter plot showing the correlation between Cs and eta1. The higher variability of the Cs estimate is related to the correlation. The second frame shows the parameters derived from fits to the intensity SDF. The excess Cs variabilit and he correlation are gone. However, the intensity parameter estimation is more sensitive to the initiation procedure.
The basic structure and dynamics of the ionosphere are captured by deterministic models. At the next level, physics-based ionospheric simulations produce stochastic structure, which is characterized by a statistical model. Statistical models characterize an ensemble of realizations that support well-defined average measures, such as means, higher moments, probability density functions, and covariance. Such models require statistical uniformity, whereas real processes not strictly homogeneous.
Analyzing real diagnostic data requires segmentation and averaging. The length of the segment and the sample interval determine the scale or frequency measurement range. Selecting a segmentation requires and assessment of the largest scale that supports statistical substructure. In our 2014 paper Wavelet-based analysis and power law classification of C/NOFS high-resolution electron density data, REF wavelets were introduced because of their ability to measure the variation of the scale over as many scale replications supported by the interval. Scale spectra measure scale versus distance, and thereby provide scale measures and scale dependent uniformity. A classification procedure was then developed to estimate two-component power-law parameters.
In a second study the classification procedure was applied to C/NOFS data accumulated over a four-year period REF. It was found that the most highly disturbed passes supported two-component power-law, giving way to a single power-law at smaller disturbance levels. All the classified SDFs showed a correlation between the turbulent strength and the large-scale spectral index. It had also been noted that the correlation was observed in remote diagnostics as well.
Because of the persistence of the correlation between the turbulent strength and the large-scale power-law index and some published papers discovered in development of Maximum Likelihood IPE, we began to suspect that the correlation was intrinsic to power-law parameter estimation. A detailed study, which has been submitted for publication, REF, show that this was indeed the case.
It was shown further that wavelet-based estimators exaggerate the correlation. The ramifications for the C/NOFS results change mainly the interpretation. The correlation is intrinsic power-law measurements, not a property of the underlying structure. Regarding wavelets, we believe they are useful for identifying segmentation, but should not be used in place of periodograms for IPE.
Simplified models that capture the essential elements of physical phenomena are used extensively. The equivalent phase-screen model is a case in point, but the approximation is not overly constraining. As as long as the structure encountered is statistically uniform or slowly varying along the propagation path, scintillation well removed from the structured region is statistically indistinguishable from a full-diffraction simulation. However, two-dimensional propagation is fundamentally different from three-dimensional propagation. For example, phase screens with no variation along one direction launch cylindrical waves, which vary as 1/r.
A compelling reason for using two-dimensional models is that diagnostic measurements are time series. As shown in the book Chapter 4, an effective scan velocity converts the time to spatial distance within a two-dimensional field. Propagation from a one-dimensional phase screen generates a one-dimensional field that can be compared directly to a diagnostic data. The two-dimensional phase-screen theory provides a complete model of one-dimensional scintillation from a phase-screen with prescribed power-law parameters. Moreover, there is a closed-form solution for the intensity spectral density function SDF.
With a combination of asymptotic approximations and numerical integration, Charlie Carrano developed a very efficient calculation of the intensity SDF REF In the reference he also demonstrated an irregularity parameter estimation (IPE) scheme to find the parameters that provided a best match to a measured SDF. The initial goodness of fit measure was the least squares error of the logarithms of the measured and theoretical SDFs. A more refined Maximum Likelihood goodness-of-fit measure was later introduced REF.
To the extent that IPE generates parameters that match real data, a phase-screen model can be used to generate frequency-dependent scintillation realizations for system analysis. The paper “A compact multi-frequency GNSS scintillation model,” published in the Institute of Navigation Journal describes such a model for GPS scintillation. Cited references demonstrate validation. A MatLab implementation of the model can be down loaded from github.com.
This website has been dormant since 2015. The website was started as a platform for discussion related to my book published in 2011. I have removed some of the blogs, which are out of date. Blogs that clarified topics in the book, identified errors, and introduced related topics have been retained.
To put this in perspective, the first two book chapters laid the foundation for a complete theory of scintillation, which follows from the forward propagation equation (FPE). Briefly, for propagation studies Maxwell’s equations are used to derive second-order differential equations that characterize electromagnetic (EM) wave propagation, which are known to engineers as the Helmholtz equation. However, the Helmholtz equation characterizes EM fields emanating from a collection of interacting point sources. The problem of interest involves calculating the propagation of an EM field from the phase center of a transmitting antenna to the phase center of a receiving antenna.
To put the Helmholtz equation in a more directly applicable form, it is rewritten as a pair of coupled first-order differential equations that individually characterize EM waves propagating in opposite directions along the reference direction defined by the ray connecting antenna phase centers. A well-designed radio transmission and reception system will maximize the energy collected at the receiver. The FPE characterizes the field launched at the transmitter the intercepts the phase center of the receiving antenna. A further simplification calculates time-harmonic fields, which generally capture all that is needed to calculate signal amplitude, phase, and delay perturbations. The FPE is exceptionally well suited for calculating propagation effects induces by ionospheric structure intercepted along the propagation path.
As a first-order differential equation, the FPE can be integrated to generate a realization of the propagating EM field. However, his requires a model of the ionospheric structure. This information comes from three sources:
Only purely statistical models were introduced in the book. To accommodate field-aligned anisotropy, the spherical isotropic surfaces of constant spatial coherence are transformed into elongated surfaces, generally ellipsoids. Additionally, because the transmission paths of primary interest were from earth-orbiting satellites to near-earth receivers, an ionospheric topocentric coordinate system with downward, northward, and eastward reference axes was introduced. In a downward oriented coordinate system satellite to earth propagation paths intercept the earth’s surface a very large distances from the nadir point. For efficient computation the integration is performed in a continuously displace coordinate (CDP) system that follows the reference ray. Chapter 4 in the book developed all the necessary geometric manipulations. The oblique propagation blog introduces supplemental material to clarifying how CDP coordinates are introduced into moment equations.
While scintillation theory follows from solutions to the FPE, characterizing stochastic structure requires statistical measures. Statistically homogeneous processes are characterized by spectral density functions (SDFs), which is formally ensemble averages of the intensity of spatial Fourier transformations of the structure realizations. Chapter 3 reviews the most widely used statistical theory, which introduces a hierarchy of differential equations that statistical observables to functions of the structure SDF. While much has been learned from solutions to the fourth-order moment equation that characterizes intensity scintillation, the computation involved is too demanding for interpreting diagnostic measurements.
A time-honored simplification is the equivalent phase screen, which concentrates the structure into an equivalent path-integrated phase screen. Under the narrow-angle scatter or parabolic approximation forward propagation is completely specified by the Fresnel scale. The scintillation at a fixed distance from the phase screen is reproduced at a different frequency and propagation distance that keeps the Fresnel scale constant. The FPE becomes the more familiar parabolic wave equation (PWE). Moreover, the scintillation intensity SDF (and scintillation index S4) can be computed a function derived from the structure SDF. The Phase Screen Models for Numerical Computation blog includes a compact summary of the material.
The material in Chapter 4 influenced the development of a simulation model called SIGMA Dispande. The phase-screen model was used to simulate the GPS effects of scintillation on GPS signals Ghafoori
Chapter 5 addresses system applications, which include signal processing for scintillation diagnostics. Beacon satellite diagnostic receivers transmit VHF, UHF, and L-band signals. Digital receives generate frequency-dependent amplitude and phase histories. The phase data are dominated by changing range, which can introduce Doppler shifts exceeding 12 kHz. To measure the scintillation component, it is necessary to isolate the Doppler component. One method is to implement a digital phase locked loop (PLL). However, the order of the PLL determines the number of samples used to estimate the frequency or phase. A more robust procedure that allows an arbitrary number of samples is described in the Digital Signal Processing and A Comparison of Phase Locked Loops and Frequency Hypothesis Testing blogs. The blog AGU 2013 Poster and Supplemental Material describes a true tomographic reconstruction, which is mainly of academic interest because of the sampling requirements.
Chapter 5 also introduced some diagnostic signal processing procedures and a supplemental MatLab library. Simulated complex scintillation requires no detrending. For plane-wave excitation the average signal intensity is constant, which is most conveniently set to unity. Real intensity scintillation measurements vary because of path-loss associated with changing range and antenna pattern variations. A Butterworth filter is typically used to make a rigid frequency separation between the signal mean and the structure component. One problem with this approach is that the detrend interval should be data driven and an large as possible. While it is true that Fresnel filtering suppresses large scale variation, the cutoff is not rigid and level dependent. We find that wavelet-based filters are easier to implement and more flexible. Simulated phase scintillation requires no detrending. Real phase scintillation data is dominated by the geometric path variation. The problem there is you cannot separate the geometric contribution from total electron content variation, which is the reason navigation satellites use multi-frequency transmissions. These issues will be discussed in separate blog entries.
What amounts to a GPS Toolbox, which is an upgrade of resources originally developed for low-earth-orbit (LEO) beacon data, contains orbit prediction from ephemeris elements, magnetic field computation, and GPS coordinate manipulation. Scintillation utilities provide all the geometric transformations needed to accommodate field-aligned geometry dependencies. A wavelet library provides all the MatLab utilities needed for wavelet based detrending and segmentation applications.
